Sistema de Ecuaciones Lineales

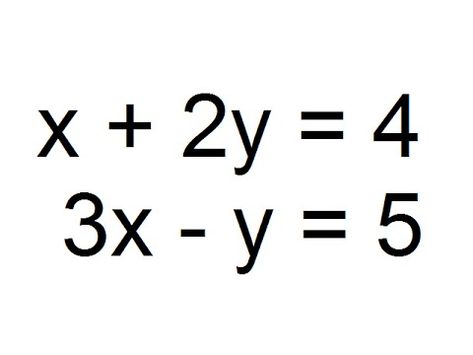
Un sistema de ecuaciones lineales puede entenderse como un modelo matemático formal que describe la interacción simultánea entre varias magnitudes desconocidas mediante relaciones de tipo lineal. Cada ecuación que compone el sistema representa una condición específica que deben cumplir las incógnitas, y el conjunto completo de ecuaciones impone restricciones que actúan de manera conjunta. A diferencia de una ecuación aislada, el interés del sistema radica en que las incógnitas no se analizan de forma independiente, sino como variables interrelacionadas dentro de una misma estructura algebraica.

En el caso particular de un sistema formado por dos ecuaciones con dos incógnitas, usualmente representadas por las variables x e y, cada ecuación define una relación lineal entre ambas variables. Desde un punto de vista geométrico, estas ecuaciones pueden interpretarse como rectas en el plano cartesiano, y el sistema completo describe la manera en que dichas rectas se posicionan entre sí. Así, el análisis del sistema no solo es algebraico, sino también conceptual, ya que permite comprender cómo distintas condiciones pueden coexistir o entrar en conflicto.

Resolver un sistema de ecuaciones lineales implica determinar los valores de las incógnitas que satisfacen simultáneamente todas las ecuaciones que lo componen. Es decir, se busca un conjunto de valores que haga verdaderas todas las relaciones establecidas en el sistema. Este proceso no siempre conduce a un único resultado, ya que la compatibilidad entre las ecuaciones depende de la coherencia de las relaciones que describen.

En algunos casos, las ecuaciones pueden ser inconsistentes entre sí, lo que significa que no existe ningún conjunto de valores que satisfaga todas las condiciones al mismo tiempo. En otras situaciones, las ecuaciones pueden resultar equivalentes o dependientes, lo que da lugar a una cantidad infinita de soluciones posibles. Cuando, por el contrario, las ecuaciones son independientes y compatibles, el sistema admite una única solución bien definida. En este último caso, se dice que el sistema es compatible determinado, ya que existe un valor específico para cada incógnita que cumple simultáneamente todas las ecuaciones planteadas.

Cómo resolver una ecuación lineal

Para que un sistema de ecuaciones lineales posea una solución única, es imprescindible que el número de ecuaciones independientes sea, como mínimo, igual al número de incógnitas presentes. Cada ecuación introduce una restricción adicional sobre los valores posibles de las variables, y solo cuando estas restricciones son suficientes y no redundantes es posible determinar un conjunto único de valores. Si faltan ecuaciones, el sistema queda incompleto y no puede fijar de manera precisa todas las incógnitas; en cambio, cuando existe correspondencia entre el número de ecuaciones y de variables, el sistema puede resolverse de forma exacta.

Método de sustitución

El método de sustitución se basa en aislar una de las incógnitas en una de las ecuaciones del sistema, expresándola en función de la otra variable. Esta expresión se reemplaza posteriormente en la ecuación restante, lo que transforma el sistema original en una única ecuación lineal con una sola incógnita. Una vez resuelta dicha ecuación, se obtiene el valor de una de las variables, que luego se sustituye en la expresión inicial para calcular el valor de la segunda incógnita. Este procedimiento permite reducir gradualmente la complejidad del problema.

Sea el siguiente sistema de ecuaciones lineales:

Primero se sustituye el valor de y en la primera ecuación:

x + 4 = 10

Resolviendo la ecuación, se obtiene:

x = 6

La solución del sistema es x = 6 e y = 4.

Método de reducción

El método de reducción consiste en combinar algebraicamente las ecuaciones del sistema mediante operaciones como la suma o la resta, con el objetivo de eliminar una de las incógnitas. Para lograrlo, puede ser necesario multiplicar previamente alguna ecuación por una constante adecuada. Al desaparecer una variable, se obtiene una ecuación con una sola incógnita, cuya resolución es directa. Posteriormente, el valor hallado se utiliza para determinar la incógnita restante sustituyéndolo en una de las ecuaciones originales.

Consideremos el siguiente sistema de ecuaciones:

Sumando ambas ecuaciones, la incógnita y se elimina:

2x = 10

Resolviendo:

x = 5

Sustituyendo este valor en la primera ecuación:

5 + y = 8

y = 3

La solución del sistema es x = 5 e y = 3.

Método de igualación

El método de igualación se fundamenta en despejar la misma incógnita en ambas ecuaciones del sistema. Al hacerlo, se obtienen dos expresiones que representan el mismo valor, por lo que pueden igualarse entre sí. Esta igualdad conduce a una ecuación con una sola incógnita, que al resolverse proporciona el valor de una de las variables. Finalmente, dicho valor se sustituye en cualquiera de las expresiones iniciales para obtener el valor de la otra incógnita. Este método destaca por su énfasis en la coherencia entre las ecuaciones del sistema.

M.R.E.A.

Administración desde Cero

.