¿Qué son los polinomios?
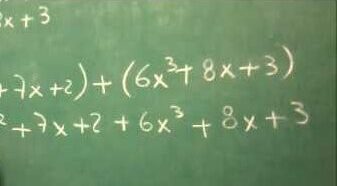
Un polinomio es un objeto fundamental del álgebra que se utiliza para representar relaciones cuantitativas entre magnitudes. Desde un punto de vista matemático, un polinomio es una expresión algebraica construida mediante un número finito de operaciones de suma, resta y multiplicación, en las que intervienen constantes numéricas, variables simbólicas y exponentes enteros positivos. La ausencia de divisiones por variables, exponentes negativos o fraccionarios es una condición esencial para que una expresión sea considerada un polinomio.
Las variables representan cantidades cuyo valor puede cambiar y suelen expresarse mediante letras, como x, y o z. Las constantes son valores numéricos fijos que no dependen de las variables, y pueden ser números enteros o fraccionarios. Los exponentes indican cuántas veces una variable se multiplica por sí misma y, en el contexto de los polinomios, deben ser siempre números enteros positivos. Esta restricción garantiza que la estructura del polinomio sea estable y que su comportamiento matemático sea predecible.
Un polinomio está compuesto por un conjunto finito de términos. Cada término es una combinación de una constante, una o varias variables y sus respectivos exponentes, todos ellos relacionados únicamente mediante multiplicación. Por ejemplo, una constante aislada, una constante multiplicada por una variable o una constante multiplicada por varias variables elevadas a determinadas potencias son expresiones que constituyen términos válidos. Los términos se distinguen entre sí porque están separados por signos de suma o resta, lo que permite identificar claramente cada componente del polinomio.
La organización y manipulación de los polinomios requieren un análisis cuidadoso de sus términos. Para simplificar, sumar o restar polinomios, es necesario agrupar aquellos términos que poseen exactamente las mismas variables elevadas a los mismos exponentes. Estos se denominan términos semejantes y pueden combinarse mediante la suma o resta de sus coeficientes numéricos. Por ejemplo, los términos que contienen únicamente la variable x pueden agruparse entre sí, al igual que los términos que contienen la variable y o aquellos que no contienen ninguna variable.
Además, el signo que precede a cada término cumple un papel crucial, ya que determina la operación que se realiza al combinarlo con los demás términos del polinomio. Una correcta interpretación de estos signos es indispensable para evitar errores en los cálculos algebraicos.
Tipos de polinomios
La clasificación de los polinomios se fundamenta en el número de términos que los componen, ya que esta característica permite describir de manera precisa su estructura algebraica y facilita su estudio y manipulación. Cada término representa una combinación específica de constantes y variables, y el conjunto de estos términos, unidos por operaciones de suma o resta, determina la complejidad del polinomio.
Cuando una expresión algebraica está formada por un solo término, se denomina monomio. En este caso, no existen operaciones de suma o resta internas, sino únicamente una multiplicación entre una constante y una o varias variables elevadas a exponentes enteros positivos. Los monomios constituyen la forma más simple de los polinomios y funcionan como los bloques básicos a partir de los cuales se construyen expresiones algebraicas más complejas.
Si la expresión contiene exactamente dos términos separados por una suma o una resta, recibe el nombre de binomio. En los binomios ya se observa una interacción entre términos distintos, lo que permite representar relaciones algebraicas más variadas que las de un monomio. La presencia de dos términos hace posible el análisis de diferencias, incrementos o contrastes entre magnitudes representadas por las variables.
Un polinomio formado por tres términos se clasifica como trinomio. Este tipo de expresión es especialmente relevante en el álgebra, ya que aparece con frecuencia en factorizaciones, ecuaciones cuadráticas y modelos matemáticos básicos. La combinación de tres términos permite describir relaciones más ricas y equilibradas entre constantes y variables, ampliando las posibilidades de interpretación y resolución.
Cuando una expresión algebraica posee más de tres términos, se le denomina de manera general polinomio, sin una designación específica basada en el número de términos. Estos polinomios de mayor extensión pueden representar fenómenos más complejos y requieren procedimientos algebraicos más elaborados para su simplificación o análisis. En todos los casos, la clasificación según el número de términos proporciona un marco conceptual claro que ayuda a comprender la estructura del polinomio y a aplicar correctamente las técnicas matemáticas correspondientes.
Grado de un polinomio
El concepto de grado de un polinomio es esencial en el estudio del álgebra, ya que permite medir el nivel de complejidad de una expresión algebraica y anticipar su comportamiento matemático. El grado está directamente relacionado con los exponentes de las variables que aparecen en los monomios que conforman el polinomio, y su determinación varía según se trate de expresiones con una sola variable o con varias variables.
En el caso de un polinomio de una sola variable, el grado se define como el mayor exponente con el que aparece dicha variable. Por ejemplo, en la expresión

el exponente más alto de la variable x es cuatro, por lo que el grado del polinomio es cuatro. Esta definición es sencilla porque todas las potencias se refieren a la misma variable y basta con identificar el exponente máximo.
Para comprender mejor este concepto, conviene analizar primero los monomios, que son los elementos básicos de los polinomios. Si un monomio contiene una sola variable acompañada de un exponente, su grado coincide exactamente con ese exponente. Por ejemplo, el monomio
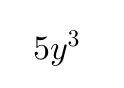
tiene grado tres, ya que la variable y aparece elevada a la tercera potencia.
Cuando un monomio incluye dos o más variables, cada una de ellas posee un grado relativo, que corresponde al exponente que la acompaña. Por ejemplo, en el monomio
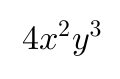
la variable x tiene grado relativo dos y la variable y tiene grado relativo tres. Sin embargo, para determinar el grado absoluto del monomio, que es el que se utiliza para clasificar polinomios, se suman todos los exponentes de las variables presentes. En este caso, el grado absoluto es cinco, resultado de sumar dos más tres.
Si alguna variable no presenta exponente escrito, se asume que su exponente es uno. Por ejemplo, en el monomio
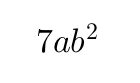
la variable a tiene exponente uno y la variable b tiene exponente dos. Al sumar estos valores, se obtiene un grado absoluto de tres. Este criterio garantiza que todas las variables contribuyan al grado total del monomio, incluso cuando su exponente no se expresa de manera explícita.
Un polinomio está formado por varios monomios, también llamados términos. Para hallar el grado de un polinomio con una o varias variables, se determina primero el grado absoluto de cada uno de sus términos y luego se identifica el mayor de ellos. Por ejemplo, consideremos el polinomio:
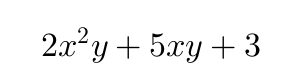
El monomio 2x^{2}y tiene grado absoluto tres, el monomio 5xy tiene grado dos y el término constante 3 tiene grado cero, ya que no contiene variables. En consecuencia, el grado del polinomio es tres, que corresponde al mayor grado entre sus términos.
Cuando los monomios que integran un polinomio no son semejantes entre sí, es decir, no comparten las mismas variables con los mismos exponentes, se dice que el polinomio se encuentra en forma reducida. Cada uno de estos monomios recibe el nombre de término del polinomio. El término que posee el mayor grado se denomina término principal, y el número que lo acompaña se llama coeficiente principal. Por ejemplo, en el polinomio
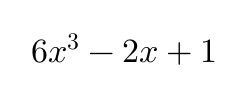
el término principal es 6x^{3} y su coeficiente principal es seis.
Si un polinomio incluye un término que no contiene variables, como el número uno en el ejemplo anterior, dicho término recibe el nombre de término independiente. Finalmente, se define el grado del polinomio como el mayor de los grados de sus monomios, ya que este valor permite clasificar las ecuaciones algebraicas y determinar los métodos adecuados para su resolución. Conocer el grado de un polinomio es fundamental para comprender su estructura, su comportamiento gráfico y las técnicas matemáticas necesarias para su análisis.
M.R.E.A.