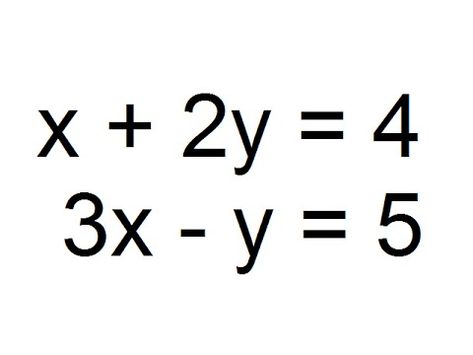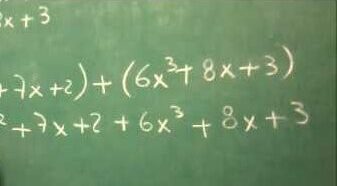Conceptos básicos del álgebra

El conocimiento del álgebra constituye un paso fundamental en la formación matemática, ya que permite trasladar el pensamiento cuantitativo desde situaciones concretas hacia representaciones abstractas mediante símbolos y expresiones. Comprender los conceptos de la matemática no se limita a memorizar fórmulas o realizar cálculos mecánicos; implica desarrollar la capacidad de interpretar relaciones, patrones y estructuras que subyacen en distintos fenómenos.
El lenguaje algebraico, que utiliza letras, signos y operaciones para representar cantidades y relaciones desconocidas, se convierte en una herramienta poderosa para analizar y resolver problemas. Este lenguaje permite generalizar situaciones específicas, facilitando la comprensión de problemas que, de otro modo, resultarían complejos si se abordaran únicamente con números concretos. Por ejemplo, situaciones cotidianas como calcular presupuestos, distribuir recursos, analizar tendencias o estimar resultados pueden expresarse mediante ecuaciones o desigualdades, mostrando que la utilidad del álgebra trasciende el aula y se extiende a contextos sociales, económicos, científicos y tecnológicos.
Además, el aprendizaje del álgebra fomenta habilidades cognitivas como la lógica, el pensamiento crítico y la resolución sistemática de problemas, al requerir que el estudiante identifique variables, relaciones funcionales y procedimientos de transformación de expresiones. La comprensión profunda del lenguaje algebraico no solo prepara al individuo para estudios avanzados en matemáticas, física, química y otras ciencias, sino que también contribuye a desarrollar una manera estructurada y analítica de enfrentar desafíos cotidianos, promoviendo la capacidad de tomar decisiones fundamentadas y de modelar situaciones reales mediante herramientas matemáticas.
Comprender los conceptos básicos es esencial porque el álgebra no solo se ocupa de números concretos, sino también de símbolos que representan cantidades desconocidas o variables. Este nivel de abstracción permite modelar situaciones diversas de la vida cotidiana, desde cálculos financieros hasta fenómenos científicos y tecnológicos, proporcionando herramientas para analizar, generalizar y predecir resultados.
Además, los conceptos básicos fomentan el desarrollo de habilidades cognitivas como el razonamiento lógico, la resolución sistemática de problemas y la capacidad de identificar patrones. Aprender a manejar correctamente operaciones y expresiones algebraicas en este nivel inicial es crucial, ya que sienta las bases para la resolución de ecuaciones, la interpretación de funciones y la comprensión de estructuras matemáticas más complejas en etapas avanzadas.
Lenguaje algebraico
El lenguaje algebraico representa uno de los pilares fundamentales del pensamiento matemático, ya que permite trasladar ideas y relaciones cuantitativas de la realidad a un sistema simbólico preciso y manejable. A diferencia de las operaciones aritméticas básicas, que trabajan con números concretos, el lenguaje algebraico utiliza símbolos, letras y expresiones para representar cantidades conocidas y desconocidas, así como las relaciones que existen entre ellas. Esta capacidad de generalización convierte al álgebra en una herramienta universal para describir patrones, formular reglas y modelar situaciones complejas que no podrían resolverse únicamente mediante números específicos.
El dominio del lenguaje algebraico implica comprender no solo los símbolos individuales, como variables y constantes, sino también la manera en que estos se combinan mediante operaciones, propiedades y estructuras. La letra x, por ejemplo, puede representar una cantidad que varía, un valor desconocido o una medida que se repite en distintos contextos. En el lenguaje algebraico se recurre al uso de letras para representar números cuando su valor no es conocido, cuando puede variar o cuando se desea expresar una relación general válida para muchos casos. Esta práctica no es arbitraria, sino una necesidad lógica del razonamiento matemático.
Al emplear letras como a, b, c o d, se logra abstraer el concepto de número y trabajar con estructuras generales. De este modo, una misma expresión puede describir infinitas situaciones numéricas concretas sin perder precisión ni rigor. Las letras funcionan como símbolos que pueden asumir distintos valores, lo que permite formular leyes, propiedades y relaciones matemáticas de alcance universal.
Esta abstracción facilita el análisis de relaciones funcionales, la construcción de ecuaciones y desigualdades, y el desarrollo de estrategias de resolución aplicables a una amplia variedad de problemas, desde cálculos financieros hasta fenómenos físicos o sociales. Además, el lenguaje algebraico fomenta el pensamiento lógico y el razonamiento deductivo. La necesidad de seguir reglas para manipular símbolos y transformar expresiones exige al estudiante organizar su pensamiento de manera sistemática y anticipar los resultados de sus operaciones.
Esta estructura lógica no solo es útil dentro de la matemática, sino que también fortalece habilidades cognitivas aplicables a la resolución de problemas en otras disciplinas y en la vida cotidiana, como la planificación, la predicción y la optimización de recursos.
En el ámbito educativo, introducir el lenguaje algebraico permite al estudiante pasar de un enfoque concreto y numérico a uno abstracto y general, estableciendo las bases para el estudio de ecuaciones, funciones, gráficos y sistemas de relaciones más complejos. Asimismo, proporciona las herramientas necesarias para modelar fenómenos reales, interpretarlos y encontrar soluciones de manera sistemática, lo que convierte al álgebra en un instrumento indispensable para la comprensión y el análisis del mundo que nos rodea.
Vocabulario básico del álgebra
El álgebra posee un vocabulario propio que describe con exactitud las operaciones matemáticas y las relaciones entre cantidades. Comprender el significado de estos términos es fundamental para interpretar y construir expresiones algebraicas correctamente.
Factor y producto
El término factor se refiere a cada uno de los elementos que intervienen en una multiplicación. Si se multiplica una cantidad por otra, ambas reciben el nombre de factores, ya que contribuyen conjuntamente a formar el resultado.
Ejemplo: en la multiplicación 3x · 4y, los factores son 3x y 4y.
El producto es el resultado de una multiplicación. Cuando dos o más números se multiplican, el valor obtenido expresa la magnitud conjunta de esos factores.
Ejemplo: el producto de 3x · 4y es 12xy.
Suma, resta y diferencia
La suma es el resultado de añadir dos o más cantidades. En álgebra, la suma permite combinar valores para obtener una cantidad total.
Ejemplo: la expresión x + 5 representa la suma de x y 5.
La diferencia es el resultado de una resta. Indica cuánto excede una cantidad a otra o cuánto falta para igualarlas.
Ejemplo: la diferencia entre a y b se expresa como a − b.
La resta es la operación mediante la cual se calcula una diferencia, es decir, se sustrae una cantidad de otra.
Ejemplo: al restar 7x − 2x se obtiene 5x.
División, cociente y residuo
La división es la operación que consiste en repartir una cantidad en partes iguales o en determinar cuántas veces una cantidad está contenida en otra.
Ejemplo: la división de 12x entre 3 se escribe como 12x / 3.
El cociente es el resultado de una división. Representa la relación entre el número que se divide y el número por el cual se divide.
Ejemplo: el cociente de 12x / 3 es 4x.
El residuo es la cantidad que sobra cuando una división no es exacta. Indica la parte que no pudo distribuirse de manera uniforme.
Ejemplo: al dividir 7x entre 3, se obtiene 2x como cociente y x como residuo.
Razón y potenciación
La razón expresa una comparación entre dos cantidades mediante una división. Permite analizar la proporción existente entre ellas.
Ejemplo: la razón entre a y b se expresa como a / b.
El cuadrado de un número es el resultado de multiplicar ese número por sí mismo. Esta operación es un caso particular de la potenciación.
Ejemplo: el cuadrado de x es x² = x · x.
La potenciación es la operación mediante la cual un número, llamado base, se multiplica por sí mismo tantas veces como indique un número natural llamado exponente.
Ejemplo: a³ = a · a · a.
Traducción del lenguaje verbal al lenguaje algebraico
En el lenguaje algebraico, las expresiones verbales se traducen en formas simbólicas precisas:
La suma del cuadrado de dos números se expresa como el cuadrado del primer número más el cuadrado del segundo.
Ejemplo: a² + b².
El doble producto de dos números se representa multiplicando ambos números y luego multiplicando el resultado por dos.
Ejemplo: 2xy.
El doble de la suma de dos números indica que primero se suman las dos cantidades y luego se multiplica el resultado por dos.
Ejemplo: 2(a + b).
La mitad de un número se obtiene dividiendo dicho número entre dos.
Ejemplo: x / 2.
El doble de un número se expresa multiplicando ese número por dos.
Ejemplo: 2x o 2m.
El cociente de dos números se representa colocando una cantidad dividida entre otra.
Ejemplo: a / b.
Números naturales
Los números naturales constituyen la primera aproximación formal del ser humano al concepto de cantidad y conteo, y representan el conjunto más elemental de números que se utilizan para describir y organizar el mundo que nos rodea. Estos números, que comienzan generalmente desde la unidad y continúan de manera infinita, permiten expresar la idea de “cuánto” y “cuántos” de manera directa y concreta, facilitando la enumeración de objetos, eventos o elementos en una colección determinada. Su estudio es fundamental porque establece las bases sobre las cuales se construyen conceptos matemáticos más complejos, como las operaciones aritméticas, la teoría de números y posteriormente el álgebra. La expresión escrita de los números naturales, estos se representan con la letra N, en mayúscula.
Los números naturales no solo cumplen la función de contar, sino que también introducen al estudiante en la noción de orden y secuencia. Cada número tiene un lugar específico dentro de la serie, lo que permite comparar magnitudes, establecer relaciones de mayor o menor y organizar conjuntos de manera lógica. Esta característica es esencial para desarrollar habilidades cognitivas de clasificación, jerarquización y análisis sistemático de datos, competencias que trascienden la matemática y se aplican en situaciones cotidianas y científicas.
Además, el estudio de los números naturales proporciona una comprensión inicial de las operaciones básicas: la suma, la resta, la multiplicación y la división, así como de sus propiedades fundamentales, como la asociativa, conmutativa y distributiva. Estas operaciones y propiedades permiten construir estructuras algebraicas iniciales y preparar al estudiante para manejar expresiones más abstractas, resolviendo problemas que van desde la simple organización de objetos hasta situaciones más complejas de la vida diaria, como la planificación de recursos o la gestión de cantidades.
En el ámbito educativo y científico, los números naturales representan también un punto de partida para la generalización de conceptos matemáticos. La capacidad de abstraer patrones, formular reglas y aplicar razonamiento lógico tiene su primer entrenamiento en el manejo de estos números. Por ello, comprender profundamente los números naturales no es solo aprender a contar, sino desarrollar un pensamiento estructurado, analítico y sistemático que será indispensable en el aprendizaje de conjuntos numéricos más amplios y en el dominio del lenguaje algebraico.
Números enteros
Los números enteros constituyen uno de los conjuntos fundamentales dentro de la estructura de los sistemas numéricos utilizados en matemáticas. Su aparición responde a la necesidad de extender el alcance de los números naturales, los cuales resultan insuficientes para describir situaciones en las que intervienen pérdidas, disminuciones, deudas o magnitudes que se sitúan por debajo de un punto de referencia establecido. Desde una perspectiva formal, el conjunto de los números enteros está integrado por todos los números naturales, sus opuestos o inversos aditivos negativos y el cero, y se representa convencionalmente mediante el símbolo Z, proveniente del término alemán Zahlen, que significa números.
La inclusión de los números negativos y del cero permite una descripción más completa y precisa de la realidad cuantificable. Gracias a los números enteros es posible representar estados de carencia o déficit, así como variaciones que implican un descenso respecto de un nivel inicial. Un ejemplo claro de esta utilidad se observa en la medición de la temperatura, donde los valores pueden ubicarse tanto por encima como por debajo del cero, o en el ámbito económico, donde las ganancias y las pérdidas requieren signos opuestos para distinguirse con claridad. De este modo, los números enteros amplían considerablemente el campo de aplicación del cálculo matemático y facilitan la modelación de fenómenos naturales, sociales y científicos.
Desde el punto de vista de su representación gráfica, los números enteros se disponen sobre una recta numérica orientada, en la cual el cero ocupa una posición central que actúa como referencia. A la derecha del cero se ubican los números enteros positivos, que aumentan progresivamente conforme se avanza en esa dirección, mientras que a la izquierda se encuentran los números enteros negativos, cuyos valores disminuyen a medida que se alejan del origen. Esta disposición refleja de manera visual el orden de los números enteros y su carácter infinito en ambos sentidos, ya que no existe un número entero máximo ni mínimo. Los números negativos se distinguen mediante el uso del signo menos, lo que permite identificarlos y diferenciarlos de sus correspondientes positivos.
←─── -5 ─── -4 ─── -3 ─── -2 ─── -1 ─── 0 ─── 1 ─── 2 ─── 3 ─── 4 ─── 5 ───→
En cuanto a sus propiedades operativas, los números enteros pueden ser objeto de las operaciones aritméticas fundamentales: suma, resta, multiplicación y división, siguiendo reglas específicas relacionadas con el signo de los números involucrados. Estas normas garantizan la coherencia interna del sistema y permiten realizar cálculos de manera sistemática y predecible. La comprensión de dichas propiedades resulta esencial para el desarrollo posterior de contenidos algebraicos y para la resolución de problemas matemáticos de mayor complejidad.
Números racionales
Los números racionales constituyen una extensión natural de los números naturales y enteros, diseñada para representar cantidades que no siempre pueden expresarse mediante números enteros exactos. Este conjunto de números se caracteriza por incluir todas las fracciones que pueden formarse a partir de un numerador y un denominador enteros, siempre que el denominador sea distinto de cero. La inclusión de los números racionales permite describir relaciones de proporcionalidad, partes de un todo y divisiones precisas, aspectos fundamentales para el análisis matemático y la modelación de fenómenos cuantitativos en la vida cotidiana y en diversas disciplinas científicas.
El estudio de los números racionales no solo amplía el rango de cantidades que se pueden representar, sino que también introduce al estudiante en la noción de equivalencia y simplificación de fracciones, así como en la comprensión de operaciones con magnitudes fraccionarias. Estas habilidades permiten interpretar, comparar y manipular relaciones complejas entre cantidades, fomentando el desarrollo de un pensamiento lógico más sofisticado que aquel que se emplea únicamente con números naturales. Por ejemplo, al dividir un recurso en partes iguales, al calcular proporciones en recetas o al distribuir tareas o materiales, los números racionales ofrecen una herramienta precisa y sistemática para resolver problemas que requieren exactitud y equilibrio.
Asimismo, los números racionales constituyen un paso clave hacia la abstracción matemática, ya que permiten introducir conceptos como orden, densidad y periodicidad de las fracciones dentro de la recta numérica. Su estudio facilita la transición hacia expresiones algebraicas más complejas, ecuaciones y desigualdades, al ofrecer un marco en el cual las cantidades pueden variar continuamente dentro de límites determinados, sin limitarse únicamente a valores discretos. Este proceso desarrolla habilidades cognitivas como el análisis, la generalización y la capacidad de modelar situaciones, que son esenciales tanto en la educación matemática avanzada como en la resolución de problemas prácticos en ciencias, economía y tecnología.
Números reales
Los números reales constituyen el conjunto numérico más amplio que se utiliza en matemáticas y ciencias para representar magnitudes continuas, abarcando tanto a los números racionales como a los números irracionales. Este conjunto permite describir con precisión cualquier cantidad que pueda medirse, calcularse o representarse en la recta numérica, ofreciendo una base sólida para el análisis matemático, la modelación de fenómenos físicos y la resolución de problemas en contextos tanto teóricos como aplicados. Los números reales incluyen, por un lado, los números racionales, que permiten expresar cantidades fraccionarias y proporciones exactas, y por otro, los números irracionales, que representan magnitudes que no pueden expresarse como fracciones exactas, como la raíz cuadrada de dos o el número pi, introduciendo la noción de inexactitud decimal infinita y no periódica.
El estudio de los números reales es fundamental porque permite transitar del mundo discreto, representado por los números naturales y racionales, hacia un entendimiento continuo de las magnitudes. Este concepto es esencial para comprender fenómenos que no pueden subdividirse en unidades enteras o fraccionarias de manera finita, como la distancia entre dos puntos en un plano, la longitud de una curva o la variación de una magnitud física a lo largo del tiempo. La capacidad de manejar números reales proporciona al estudiante las herramientas necesarias para analizar funciones, límites, derivadas e integrales, facilitando la resolución de problemas en matemáticas avanzadas, física, ingeniería, economía y otras ciencias.
Además, los números reales fomentan la capacidad de abstracción y razonamiento lógico al introducir nociones como densidad, continuidad y límite. Comprender que entre dos números reales siempre existe otro número real, o que ciertos números no pueden expresarse mediante fracciones exactas, desarrolla habilidades cognitivas superiores, como la generalización, el pensamiento crítico y la modelación matemática de situaciones complejas. Estas competencias no solo son relevantes para la matemática formal, sino también para la interpretación y análisis de datos en contextos científicos, tecnológicos y sociales.
Polinomios
Los polinomios constituyen una de las estructuras algebraicas más fundamentales y versátiles dentro de las matemáticas. Su estudio permite representar, analizar y modelar relaciones cuantitativas de diversa complejidad mediante sumas de términos formados por variables elevadas a exponentes enteros no negativos, multiplicadas por coeficientes que pueden pertenecer a un conjunto numérico determinado, como los números reales o complejos. En términos generales, un polinomio se define como una expresión algebraica que combina estos términos de manera lineal respecto a los coeficientes y en potencia respecto a las variables, facilitando la descripción de patrones, la resolución de ecuaciones y la modelación de fenómenos continuos o discretos.
Los polinomios se clasifican según diferentes criterios, siendo uno de los más importantes el número de términos que contienen. Así, se habla de monomios cuando la expresión consta de un solo término, binomios cuando tiene dos términos, y trinomios cuando incluye tres. Cuando un polinomio tiene cuatro o más términos, se le denomina polinomio de términos múltiples o polinomio general. Esta clasificación permite al estudiante comprender la estructura interna de las expresiones algebraicas y anticipar la complejidad de operaciones como la suma, la resta, la multiplicación o la factorización de polinomios.
El grado de un polinomio es otro concepto central, que se define como el mayor exponente de la variable presente en la expresión. El grado determina no solo la complejidad de la función asociada al polinomio, sino también la naturaleza de sus raíces, el comportamiento de su gráfica y la aplicabilidad de ciertos teoremas fundamentales del álgebra, como el teorema del factor y el teorema del resto. Comprender el grado de un polinomio permite al estudiante analizar tendencias, simetrías y puntos críticos, contribuyendo a un entendimiento más profundo de su comportamiento matemático.
Los polinomios poseen propiedades algebraicas que facilitan su manipulación sistemática. Entre estas destacan la cerradura bajo la suma y la multiplicación, la existencia de un elemento neutro y la posibilidad de asociar, conmutar y distribuir términos según reglas conocidas. Estas propiedades no solo simplifican los cálculos algebraicos, sino que también son esenciales para desarrollar estrategias de resolución de problemas más complejos, como la factorización, la simplificación de expresiones y la resolución de ecuaciones polinómicas.
La división de polinomios constituye una técnica clave para descomponer expresiones algebraicas en factores más simples, lo que permite analizar raíces, simplificar fracciones algebraicas y aplicar resultados fundamentales en cálculo y álgebra avanzada. Este procedimiento puede realizarse mediante división larga o utilizando métodos más eficientes como la división sintética, siempre basado en las propiedades algebraicas fundamentales que rigen los polinomios. La habilidad para dividir polinomios no solo es esencial en la resolución de problemas matemáticos, sino también en la modelación de fenómenos físicos, financieros y de ingeniería, donde las relaciones entre variables se representan mediante expresiones polinómicas.
Sistema de Ecuaciones Lineales
Los sistemas de ecuaciones lineales constituyen una herramienta esencial en el ámbito de las matemáticas y sus aplicaciones, ya que permiten modelar simultáneamente múltiples relaciones lineales entre variables desconocidas. Un sistema de ecuaciones lineales se define como un conjunto de dos o más ecuaciones, en el que cada ecuación involucra únicamente combinaciones lineales de las variables, es decir, variables elevadas a la potencia uno y multiplicadas por coeficientes constantes. La resolución de estos sistemas consiste en encontrar los valores de las variables que satisfacen todas las ecuaciones simultáneamente, proporcionando una descripción coherente y precisa de las relaciones matemáticas subyacentes.
La clasificación de los sistemas de ecuaciones lineales depende de la naturaleza de sus soluciones. Un sistema puede ser consistente determinado, si posee una única solución que satisface todas las ecuaciones; consistente indeterminado, cuando admite infinitas soluciones que cumplen las condiciones planteadas; o inconsistente, si no existe ninguna combinación de valores que cumpla simultáneamente todas las ecuaciones. Esta clasificación es fundamental para comprender la estructura de los sistemas lineales y anticipar el comportamiento de sus soluciones, permitiendo aplicar métodos de resolución adecuados según cada caso.
Uno de los métodos más poderosos y sistemáticos para resolver sistemas de ecuaciones lineales es el método de Gauss, también conocido como eliminación de Gauss. Este procedimiento consiste en transformar el sistema original mediante operaciones algebraicas elementales en un sistema equivalente más simple, usualmente en forma triangular o escalonada, que facilita la obtención de las soluciones de manera directa y ordenada. La efectividad del método de Gauss radica en su capacidad de simplificar sistemas complejos, reduciendo el esfuerzo computacional y proporcionando una estrategia sistemática que puede aplicarse a sistemas con cualquier número de variables y ecuaciones.
El concepto de sistemas de ecuaciones equivalentes es esencial dentro de esta metodología. Dos sistemas de ecuaciones se consideran equivalentes si poseen el mismo conjunto de soluciones, aunque sus ecuaciones puedan diferir en apariencia. La identificación y construcción de sistemas equivalentes permite aplicar transformaciones algebraicas sin alterar la validez de las soluciones, lo que constituye la base del método de Gauss y de otras técnicas de resolución. Este principio asegura que las manipulaciones realizadas durante el proceso de simplificación no comprometan la coherencia matemática del sistema, garantizando resultados precisos y confiables.
Matrices y Determinantes
Las matrices constituyen una herramienta fundamental en el campo de las matemáticas y sus aplicaciones, especialmente en álgebra lineal, al proporcionar un medio organizado y sistemático para representar y manipular conjuntos de números o símbolos de manera estructurada. Una matriz se define como una disposición rectangular de elementos, organizados en filas y columnas, en la que cada posición se identifica mediante índices que indican su ubicación específica. Esta estructura permite representar relaciones complejas entre datos, sistemas de ecuaciones lineales, transformaciones geométricas, gráficos y fenómenos multidimensionales de forma clara y eficiente.
Existen distintos tipos de matrices según sus características y estructura. Entre las más relevantes se encuentran las matrices cuadradas, que tienen igual número de filas y columnas; las matrices rectangulares, con diferente número de filas y columnas; las matrices diagonales, en las que todos los elementos fuera de la diagonal principal son cero; y las matrices identidad, que funcionan como elemento neutro de la multiplicación matricial. Esta clasificación permite al estudiante comprender las propiedades particulares de cada tipo de matriz y anticipar su comportamiento en operaciones algebraicas y aplicaciones prácticas.
La matriz inversa constituye un concepto central en álgebra lineal, especialmente en la resolución de sistemas de ecuaciones lineales y en transformaciones lineales. Una matriz cuadrada posee inversa si existe otra matriz que, al multiplicarse por la original, produce la matriz identidad. La existencia de la matriz inversa permite simplificar cálculos complejos, resolver sistemas matriciales y comprender la estructura subyacente de las transformaciones lineales de manera eficiente y sistemática.
Las operaciones con matrices son el conjunto de procedimientos algebraicos que permiten combinar, transformar y manipular matrices para obtener resultados útiles en distintos contextos. Entre estas operaciones destacan la suma y la resta, que requieren matrices de igual dimensión; la multiplicación, que combina filas y columnas según reglas específicas; y la transposición, que intercambia filas por columnas. Estas operaciones, junto con la multiplicación por un escalar, constituyen la base para desarrollar técnicas más avanzadas como la factorización, la diagonalización y la resolución de sistemas de ecuaciones mediante matrices.
Las evaluaciones matriciales consisten en aplicar operaciones específicas a matrices para obtener resultados concretos, como determinar la matriz resultante de un conjunto de transformaciones, verificar propiedades algebraicas o calcular expresiones asociadas a sistemas lineales. Estas evaluaciones permiten al estudiante consolidar la comprensión conceptual y práctica de las matrices, facilitando la resolución de problemas complejos de manera organizada y precisa.
Los determinantes constituyen un instrumento esencial para analizar las propiedades de las matrices cuadradas. El determinante de una matriz proporciona información clave sobre su invertibilidad, su rango y las soluciones de sistemas de ecuaciones asociados. Este valor escalar se obtiene mediante combinaciones específicas de los elementos de la matriz y tiene aplicaciones fundamentales en áreas como cálculo de volúmenes, transformaciones lineales, geometría analítica y resolución de ecuaciones lineales mediante la regla de Cramer. La comprensión de los determinantes permite al estudiante evaluar la consistencia de sistemas de ecuaciones, estudiar el comportamiento de funciones lineales y aplicar principios de álgebra avanzada en contextos teóricos y prácticos.
Aplicaciones del álgebra
El álgebra constituye una de las ramas más versátiles y fundamentales de las matemáticas, debido a su capacidad para representar relaciones, generalizar patrones y modelar situaciones tanto abstractas como concretas. Su utilidad radica en que proporciona herramientas conceptuales y metodológicas para analizar problemas complejos mediante símbolos y estructuras algebraicas, lo que permite expresar cantidades desconocidas, establecer relaciones funcionales y encontrar soluciones de manera sistemática y lógica. A través del álgebra, se pueden identificar regularidades, prever comportamientos y optimizar procesos en diversos campos del conocimiento, desde la física y la ingeniería hasta la economía y las ciencias sociales, consolidando su importancia como instrumento científico y tecnológico.
La aplicación del álgebra en la vida cotidiana se manifiesta de múltiples formas, muchas veces de manera imperceptible pero constante. En actividades tan comunes como la planificación de presupuestos, la distribución de recursos, el cálculo de distancias y tiempos, o la determinación de proporciones en recetas y proyectos de construcción, el álgebra permite organizar la información, establecer relaciones cuantitativas y tomar decisiones fundamentadas. Asimismo, en contextos más complejos, como la gestión de inventarios, la programación de horarios, el análisis financiero o la modelación de fenómenos naturales, las herramientas algebraicas facilitan la resolución de problemas que involucran múltiples variables y condiciones simultáneas, proporcionando soluciones precisas y eficientes.
Además, el álgebra desarrolla habilidades cognitivas que trascienden lo estrictamente matemático, como el razonamiento lógico, la capacidad de generalización, el pensamiento crítico y la resolución estructurada de problemas. Estas competencias permiten abordar desafíos cotidianos y profesionales de manera sistemática, anticipando consecuencias, evaluando alternativas y seleccionando estrategias óptimas. La habilidad para traducir situaciones concretas a expresiones algebraicas y manipularlas adecuadamente constituye, por tanto, un recurso indispensable para la toma de decisiones fundamentadas y la interpretación racional de la información cuantitativa.
M.R.E.A.